 атом
атом
 ядро
ядро
 нуклон;
нуклон; 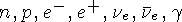
 кварки
кварки
 (????????)
(????????)
 (? ? ? ? ? ? ? ?)
(? ? ? ? ? ? ? ?)
 атом
атом
 ядро
ядро
 нуклон;
нуклон; 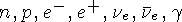
 кварки
кварки
 (????????)
(????????)
 (? ? ? ? ? ? ? ?)
(? ? ? ? ? ? ? ?)
Взаимодействия
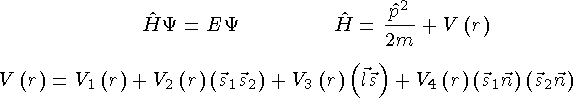
В квантовой электродинамике взаимодействие двух зарядов сводится к испусканию фотона одним зарядом и поглощение его другим. Источником фотонов является электрический заряд. Фотон - квант электромагнитного поля.
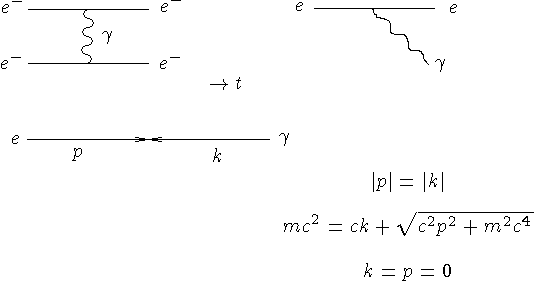
Взаимоджействие между частицами осуществляется обменом виртуальной частицей -
переносчиком взаимодействия. Для описания различных процессов с участием частиц
используют диаграммы Фейнмана. На этих диаграммах линиям со свободными концами
отвечают реальные частицы или ядра, а внутренним линиям - виртуальные частицы.
Точка, в которой рождается и поглощается виртуальная частица, называется узлом
диаграммы. Узлы диаграммы содержат основную информацию о процессе - типе
фундаментального взаимодействия и его вероятности. Линиям виртуальных частиц
сопоставляются функции распространения этих частиц, называемые пропагаторами.
Пропагатор для частицы, перносящей взаимодействие и имеющей массу 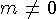 , равен
, равен 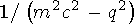 ,
где q - четырехмерный импульс частицы. Пропагатор входит множителем в амплитуду
вероятности процесса. Для того, чтобы рассчитать вероятность процесса, необходимо
прежде всего нарисовать для него все возможные диаграммы, и вычислить амплитуду
вероятности для каждой диаграммы. Полная вероятность процесса равна квадрату модуля
суммарной амплитуды для всех возможных диаграмм. Диаграммы содержат алгоритм
расчета амплитьуды процесса. Для простейших оценок достаточно помнить, что амплитуды
вероятности испускания (поглощения) частицы пропорциональна
,
где q - четырехмерный импульс частицы. Пропагатор входит множителем в амплитуду
вероятности процесса. Для того, чтобы рассчитать вероятность процесса, необходимо
прежде всего нарисовать для него все возможные диаграммы, и вычислить амплитуду
вероятности для каждой диаграммы. Полная вероятность процесса равна квадрату модуля
суммарной амплитуды для всех возможных диаграмм. Диаграммы содержат алгоритм
расчета амплитьуды процесса. Для простейших оценок достаточно помнить, что амплитуды
вероятности испускания (поглощения) частицы пропорциональна  , где
, где  - константа,
характеризующая интенсивность взаимодействия (
- константа,
характеризующая интенсивность взаимодействия (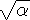 называется константой связи).
Для электромагнитного взаимодействия соответствующая константа
называется константой связи).
Для электромагнитного взаимодействия соответствующая константа 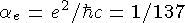 . Для диаграмм
с N узлами вероятность пропорциональна
. Для диаграмм
с N узлами вероятность пропорциональна 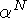 . Основная диаграмма рассеяния электрона
на ядре с зарядом Ze выглядит следующим образом (направление времени слева направо):
. Основная диаграмма рассеяния электрона
на ядре с зарядом Ze выглядит следующим образом (направление времени слева направо):
Picture
Простешие диаграммы сильного, электромагнитного и слаього взаимодействий d- и u-кварков имеют вид
Picture
//96 Если взаимодействие двух частиц осуществляется путем обмена частицей массы m, то для радиуса взаимодействия a из соотношения неопределенности можно получить оценку
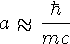
Потенциал такого взаимодействия (потенциал Юкавы) следующим образом зависит от расстояния r между частицами:
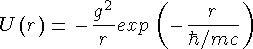 ,
,
g - заряд, присущий данному взаимодействию
(электрический - 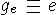 , сильный -
, сильный - 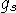 , слабый -
, слабый - 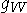 , гравитационный -
, гравитационный - 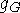 ). Если
квант поля (переносчик взаимодействия) имеет нулевую массу, то безразмерная
константа взаимодействия
). Если
квант поля (переносчик взаимодействия) имеет нулевую массу, то безразмерная
константа взаимодействия 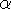 связана с зарядом соотношением
связана с зарядом соотношением 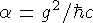 .
.
Согласно модели Юкавы, механизм ядерного взаимодействия заключается в передаче
виртуального мезона от одного нуклона к другому. Если масса виртуального мезона равна
m, то из соотношения неопределенности для радиуса взаимодействия R можно получить оценку 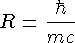 .
Зависимоть потенциала взаимодействия (потенциала Юкавы) от расстояния между частицами
имеет вид
.
Зависимоть потенциала взаимодействия (потенциала Юкавы) от расстояния между частицами
имеет вид 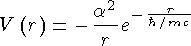 , где
, где  - константа сильного взаимодействия.
- константа сильного взаимодействия.
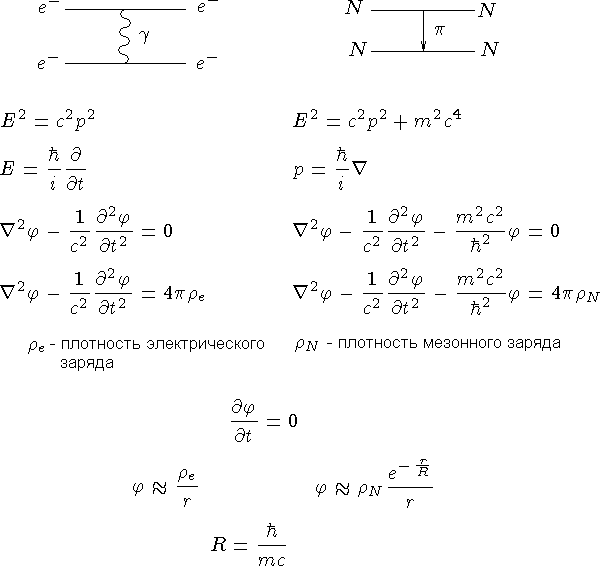
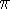 -мезоны - кванты нуклон-нуклонного взаимодействия
-мезоны - кванты нуклон-нуклонного взаимодействия
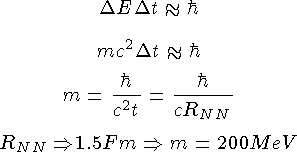
|
Частица |
Масса, |
Время жизни, |
Спин-четность, изоспин, |
||||
|
|
|
|
|
||||
|
|
|
|
|
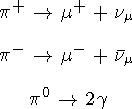
 рассеяние
рассеяние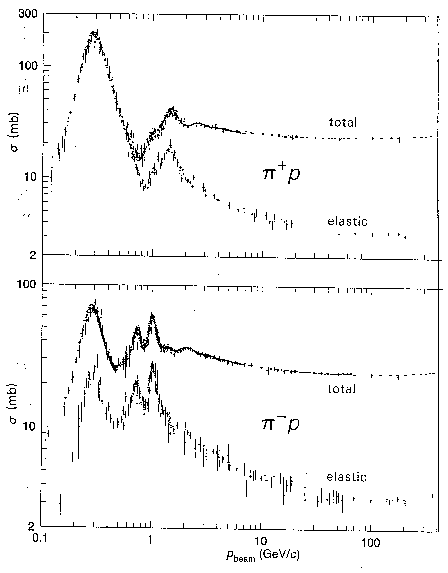
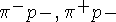 рассеяние
рассеяние
|
Система |
|
|
|||
|
|
|
|
|||
|
|
|
|
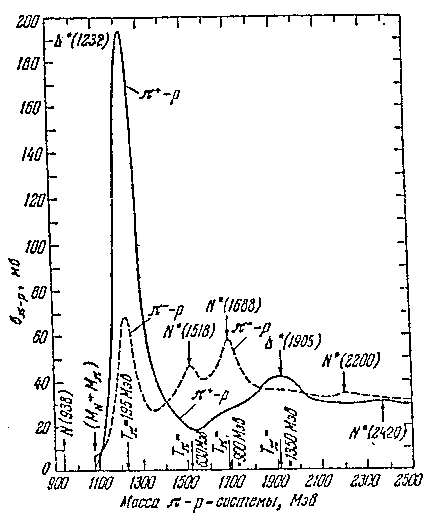
В сечении сильновзаимодействующих частиц наблюдаются резонансы - коротко живущие
возбужденные состояния адронов, распадающиеся в результате сильного взаимодействия.
Характерное время жизни резонанса 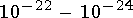 . Впервые резонансы наблюдались в сечении
взаимодействия
. Впервые резонансы наблюдались в сечении
взаимодействия 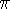 -мезонов с нуклонами. Масса резонансной частицы
-мезонов с нуклонами. Масса резонансной частицы 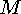 определяется из
релятивистского инварианта
определяется из
релятивистского инварианта 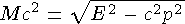 , где
, где 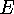 и
и 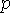 -
полная энергия и полный импульс
-
полная энергия и полный импульс 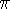 -мезона и нуклона.
Максимумы в сечении
-мезона и нуклона.
Максимумы в сечении 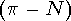 рассеяния интерпретируются как появление нестабильной частицы -
резонанса с вполне определенными квантовыми характеристиками - массой, зарядом,
спинои, изоспином и др. Резонансы наблюдаются и во взаимодействии
рассеяния интерпретируются как появление нестабильной частицы -
резонанса с вполне определенными квантовыми характеристиками - массой, зарядом,
спинои, изоспином и др. Резонансы наблюдаются и во взаимодействии 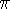 -мезонов.
-мезонов.
|
|
|
Масса, МеВ |
|
||||
|
|
|
1232 |
120 |
||||
|
|
|||||||
|
|
|
1520 |
120 |
||||
|
|
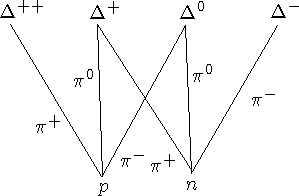
Как наблюдять резонансы
Время жизни резонанса
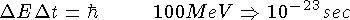
All Your comments, suggestions and bug reports (any kind) are welcome here.
Last updated 13 April 1997 year.